📖一直在入门啊

Appearance

使用torch.autograd 自动微分 ​

在训练神经网络时，最常用的算法是反向传播。在该算法中，根据损失函数相对于给定参数的梯度来调整参数（模型权重）。 为了计算这些梯度，PyTorch 有一个名为 torch.autograd 的内置微分引擎。它支持任何计算图的梯度自动计算。 考虑最简单的单层神经网络，具有输入 x 、参数 w 和 b 以及一些损失函数。它可以通过以下方式在 PyTorch 中定义：

python
import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

张量、函数和计算图 ​

该代码定义了以下计算图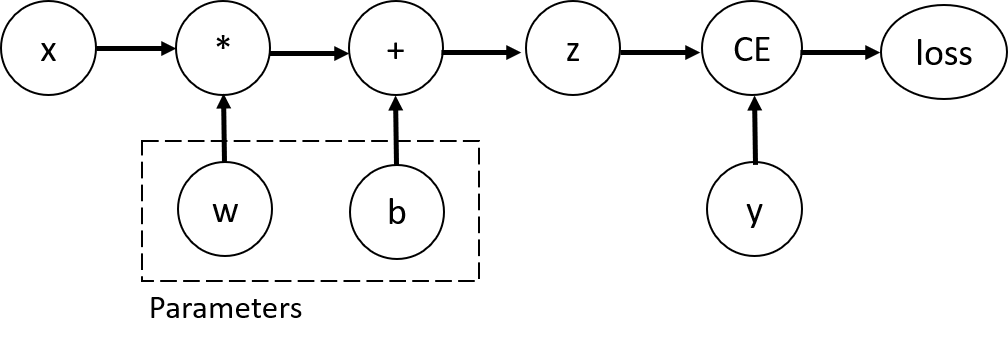： alt text

在这个网络中， w 和 b 是我们需要优化的参数。因此，我们需要能够计算损失函数相对于这些变量的梯度。为此，我们设置这些张量的 requires_grad 属性。

您可以在创建张量时设置 requires_grad 的值，或者稍后使用 x.requires_grad_(True) 方法设置。

我们应用于张量来构造计算图的函数实际上是类 Function 的对象。该对象知道如何向前计算函数，以及如何在向后传播步骤中计算其导数。对反向传播函数的引用存储在张量的 grad_fn 属性中。您可以在文档中找到 Function 的更多信息。

python
print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

out:

Gradient function for z = <AddBackward0 object at 0x7f4fd10b53c0>

Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x7f4fd108a2f0>

计算梯度 ​

为了优化神经网络中参数的权重，我们需要计算损失函数相对于参数的导数。为了计算这些导数，我们调用 loss.backward() ，然后从 w.grad 和 b.grad 检索值：

python
loss.backward()
print(w.grad)
print(b.grad)

PS：下面的暂不翻译了，原文链接：https://pytorch.org/tutorials/beginner/basics/autogradqs_tutorial.html